The previous chapter details how I built the rig to read the keypad – at this point I had all 8 connectors rigged up to 8 analogue pins on 2 different micro:bits. The image below describes how the kit was rigged:
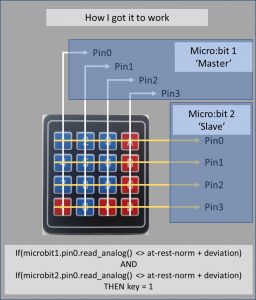
I mentioned earlier that these pins would not record a key-press on the keypad as a Boolean event, so digital read was not an option. This meant that the following, simple code, was not viable:
If (microbit1.pin0.read_digital()
and microbit2.pin0.read_digital())
then key = 1
Chapter 2 also mentions that a key-press would cause a change in the analogue reading, so my challenge was to monitor this change and infer when a key-press had occurred. I expected to get away with the following code:
If (microbit1.pin0.read_analog() > 500
and microbit2.pin0.read_analog()) > 500
then key = 1
The ‘500’ above is arbitrary (as is the greater than sign), and I expected the ideal constant to emerge in testing. This is when things got interesting, but first some terminology:
The at-rest norm. For each analogue pin there is an at-rest norm, the value that you read from that pin when there is no activity on the pin. It is different for each pin.
Deviation. Each time you read the at-rest analogue value of a pin it will differ a bit from the at-rest norm for that pin. This difference is a perturbation or deviation from the norm.
The event threshold. This is the analogue value for the pin beyond which we can state with some confidence that a key-press event has occurred.
So the challenge I had was to work out the at-rest norms and the threshold for each of the 4 pins I was using. Any reading beyond that threshold would then be a key-press. In theory a short period of trial and error should have been enough to come up with some constant values that I could use. In reality the following factors scuppered that:
- Inconsistent at-rest norms. Not only did the norms differ between pins, they differed depending on when I checked them and also how the micro:bit was powered.
- Pin3 was especially erratic. I don’t know exactly why, although it makes sense that it is related to the fact that pins0, 1 and 2 are touch pins, so I guess the capacitive element they had made a difference. Pin3 just behaved differently.
- The thresholds were hard to find and quite sensitive. I NEVER managed to come up with a set of constants that would subsume false-positives and reliably identify key-press events.
The third point above is especially relevant – false readings were untenable – the quality of the keypad would be compromised too much if false readings were constantly being thrown up. I needed a way to set the norm and the thresholds for each pin separately, and in such a way that would account for contextual circumstances that I do not have the knowledge to anticipate or mitigate against.
The image below shows output from the Mu editor across 3 different attempts to find the norm and threshold for the 4 pins I was using. These readings are all from the same micro:bit, and were taken minutes apart:
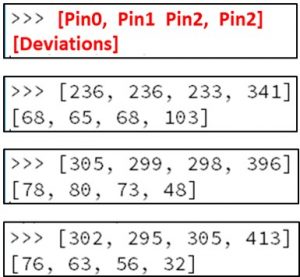
Above, the first 4 values shown are the at-rest norm for the 4 pins. The 4 values shown on the second line are the deviations from that pin (I’ll explain how I got those later in this chapter). Look at the pin3 values above:
For the first example above, a reading of 445 would show up as a key-press. This upper limit is fairly consistent across all 3. Sods law though, in 98% of the cases it is the LOWER limit that I needed to use, and these are a lot more inconsistent.
The low threshold on example 1 is 237. For the second example the lower threshold in 2 is 348 and for 3 it is 381. In theory this means that one would set the hardcoded threshold below 237. Unfortunately the actual perturbations that occur on a key-press are small, so you want the tightest threshold possible… with 237 I would lose a LOT of key-press events in examples 2 and 3.
The only solution I could see was to get the app to self-calibrate each time it was used. To do this I used the following process:
On startup 100 analogue reads of the 4 pins are made.
A simple mean (average) across 100 reads is made. The first values shown in the examples above are these means.
Each time the pins are read the difference between consecutive readings is measured. The greatest difference across all 100 events is taken as the deviation. Admittedly there are better ways to calculate deviation, but this was processor light and the values proved very useful, so I stuck with it. The second values in the image above are these deviations.
I now had a formula I could use:
If (microbit1.pin0.read_analog() < (event threshold)
and microbit2.pin0.read_analog()) < (event threshold)
then key = 1
Where event threshold = at-rest norm + deviation
Notes:
I actually used both < and > in the formulae above (so I checked the upper and lower threshold). This was necessary because in a very few number of cases a key-press would cause the analogue value to go up. Admittedly this was early on in testing and later a key-press would consistently cause the value to drop, but it was easy enough to cater for this edge case, so why not?
As mentioned, the way the deviation is measured is flawed (imagine a situation where each reading is 1 higher than the previous – across 100 readings the deviation would be 1, whereas the actual deviation from the norm would be 50). This approach was actually my first iteration, but it proved so effective I stuck with it.
I also rigged it so that the user could manually recalibrate (just click A button). So, if a lot of false readings were being made the user could get the system to amend the norms and thresholds and, ideally, eliminate the false positives.
In testing the approach above all but eliminated false positives, which means that unsolicited key-press events rarely fired. There were / are cases where actual key-presses don’t register though… they usually do on a re-click. I was OK with this – for me false positives were the evil that would kill the app, rather than occasionally needing to re-click a button to get it to register.
